环境准备
平台:windows10 64 位 IDE:Pycharm Python 版本:Python3.5 github 代码:源代码
回归的理解
回归是由高尔顿最先在生物遗传上提出的,在线性回归中,与其说其为回归,不如说线性拟合更合适,而为了纪念高尔顿还是保留了回归这一名词 而对数几率回归(Logistic regression)解决的却是一个分类问题,其实就是 2 分类,如果需要解决多分类那么就做多次 2 分类或直接用Softmax 回归。
线性回归
线性回归试图建立的一个线性模型以尽可能准确的预测输出标记。考虑最简单的模型,给定若干对$(x,y)$的数据,将其在坐标轴上表示如下:
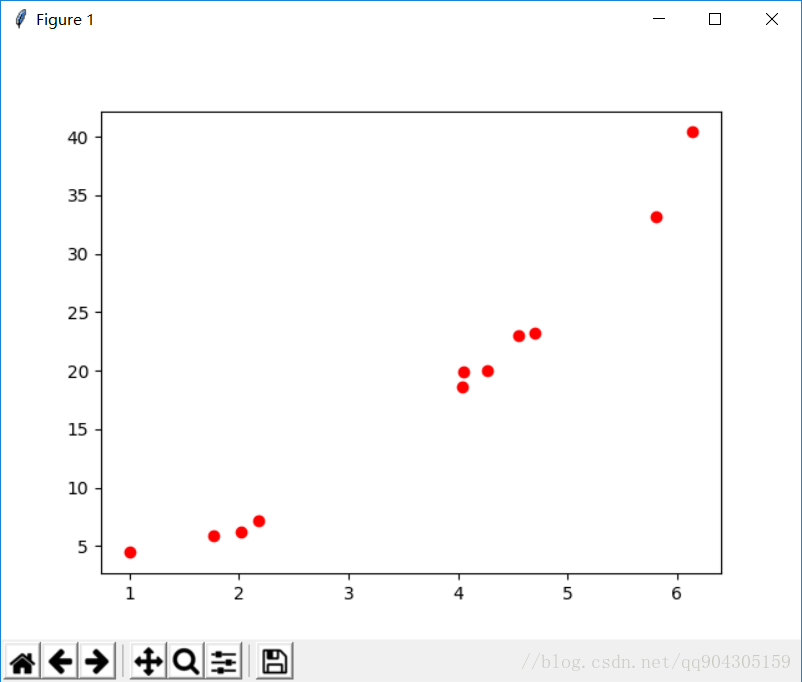 线性回归就是要寻找一条直线来使得这些所有的点都尽量符合直线上的点,其中尽量符合指的就是使损失最小,在这里以点到直线的距离的平方来作为‘损失’,使用线性回归可以来预测数据,这在机器学习里面是一个非常重要的概念——预测,不管是什么模型,最后做出来都是需要用来预测数据,来判断这个模型到底实不实用,线性回归就是这些模型中最简单的一种模型。 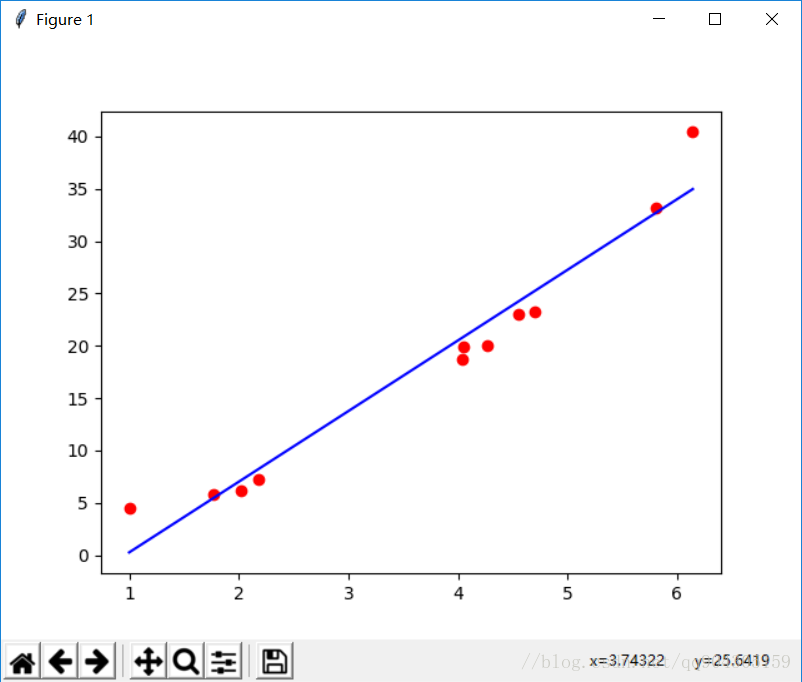 ## 使用最大似然解释最小二乘 ### 基本形式 首先对于线性回归,所求得就是一条直线,设其方程为: $$y^{(i)}=\theta^Tx^{(i)}+\varepsilon^{(i)}$$ 其中$\theta$和$\varepsilon$为这条直线的斜率和截距,$x,y$分别为图上的一系列散点,用极大似然法估计时,我们认为$\varepsilon$符合正太分布,且期望为 0,那么根据大学的知识可以得到$\varepsilon$的概率为: $$p(\varepsilon^{(i)})=\frac{1}{s\sqrt{2\pi\sigma}}exp(-\frac{(\varepsilon^{(i)})^2}{2\sigma^2})$$ 把直线方程移项带入上式得到在$\theta$参数下,已知$x$的情况下$y$的概率密度函数为: $$p(y^{(i)}|x^{(i)};\theta)=\frac{1}{\sqrt{2\pi\sigma}}exp(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2})$$ 这里的概率密度函数为条件概率密度函数,直接求解是无法解出来的,假设样本之间是独立的,那么就得到: \begin{aligned} L(\theta)&=\coprod*{i=1}^m p(y^{(i)}|x^{(i)};\theta)\\&=\coprod*{i=1}^m\frac{1}{\sqrt{2\pi\sigma}}exp(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}) \end{aligned} ### 高斯的对数似然与最小二乘 这里用的是对数似然,即需要对$L(\theta)$取对数,则可以化简得到如下方程: \begin{aligned} \ell(\theta)&=\log{L(\theta)}\\&=\log{\coprod*{i=1}^m\frac{1}{\sqrt{2\pi\sigma}}exp(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2})}\\&=\sum*{i=1}^m \log{\frac{1}{\sqrt{2\pi\sigma}}exp(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2})}\\&=m\log{\frac{1}{\sqrt{2\pi\sigma}}}-\frac{1}{\sigma^2}\cdot\frac{1}{2}\sum*{i=1}^m(y^{(i)}-theta^Tx^{(i)}) \end{aligned} 现在,需要求$L(\theta)$为最大值时$\theta$的值,前面一项为常数,可以省略掉,只保留后方一项得到函数: $$J(\theta)=\frac{1}{2}\sum*{i=1}^m(y^{(i)}-\theta^Tx^{(i)})$$ 即求$J(\theta)$的最小值,括号里的一项就是预测值和实际值之间的差,这个就成为目标函数或成为损失函数,这其实就是最小二乘估计,整个推导过程其实就是利用高斯分布推导最小二乘。 ### 向量表示下的求解 设有$M$个$N$维样本组成矩阵$X$,即$X$的行对应每个样本,$X$的列对应样本的维度,**目标函数**就可以表示为: $$J(\theta)=\frac{1}{2}\sum_{i=1}^m (h_\theta(x^{(i)})-y^{(i)})^2=\frac{1}{2}(X\theta-y)^T(X\theta-y)$$ 即现在要求出$J(\theta)$最小值时$\theta$的值,对目标函数求导,令其等于$0$,求出$\theta$的值。 \begin{aligned} \nabla*\theta J(\theta) &= \frac{1}{2}\sum*{i=1}^m(h*\theta x^{(i)}-y^{(i)})^2\\&=\nabla*\theta \left\{ \frac{1}{2} (\theta^TX^TX\theta-]theta^TX^Ty-y^TX\theta+h^Ty)\right\}\\&=\frac{1}{2}(2X^TX\theta-X^Ty-(y^TX)^T)\\&=X^TX\theta-x^Ty \end{aligned} 得到最后的结果如下: $$\theta=(X^TX)^{-1}X^Ty$$ ### L2 正则化($\ell2-norm$) 而在现实中当特征比样本点更多时,矩阵$X$不是满秩矩阵, $X^TX$不一定可逆,通常引入**正则化(egularization)**项,其实质是为了**防止过拟合**, $$ \frac{1}{2}\sum*{i=1}^m(h*\theta x^{(i)}-y^{(i)})^2+\lambda\sum\_{j=1}^n\theta_j ^2$$ 称为**$L2$正则($\ell2-norm$)**,那么加了$L2$正则的最小二乘称为**岭回归**,求解可得$\theta$为: $$\theta=(X^TX+\lambda I)^{-1}X^Ty$$ ### L1 正则化($\ell1-norm$) 既然有 L2 正则化,那么也必然有**L1 正则化($\ell1-norm$)**,将目标函数正则项中$\theta$的平方替换为$\theta$的绝对值,那么就叫 L1 正则,即**LASSO**。 $$ \frac{1}{2}\sum*{i=1}^m(h*\theta x^{(i)}-y^{(i)})^2+\lambda\sum\_{j=1}^n|\theta_j| $$ ### lastic Net 结合 l1 和 l2 正则,即为 Elastic Net: $$ \frac{1}{2}\sum*{i=1}^m(h*\theta x^{(i)}-y^{(i)})^2+\lambda(\rho\cdot\sum*{j=1}^n|\theta_j| +(1-\rho)\cdot\sum*{j=1}^n\theta_j ^2)$$ ### L1 和 L2 正则的区别 使用绝对值取代平方和,在$\lambda$最够大时,高阶的情况下高阶项的系数会缩减到 0 ## 梯度下降法 求出目标函数了,就要根据目标函数来求的这条直线,这里常用的一种方法就是梯度下降法,梯度下降法的公式如下: $$\theta=\theta-\alpha\cdot\frac{\partial J(\theta)}{\partial\theta}$$ 其中$\alpha$表示学习率,$\theta$为参数,具体做法就是初始化$\theta$,然后沿着负梯度方向迭代,不断更新$\theta$使就$J(\theta)$最小。 ## 程序分析 ```python import numpy as np import matplotlib.pyplot as plt np.random.seed(0) x = np.linspace(0, 6, 11) + np.random.randn(11) x = np.sort(x) y = x ** 2 + 2 + np.random.randn(11) ``` 首先生成随机点 x,y,随机生成 11 个点,这 11 个点是根据 y=x2+2 这条曲线上生成的。 ```python def optimizer(): w = 0 b = 0 for i in range(1000): w, b = compute_gradient(w, b, 0.02) # if i % 50 == 0: # plt.plot(x, x * w + b, 'b-') # plt.pause(0.5) y_pre = x * w + b print(w, b) return y_pre ``` 这个函数是执行梯度下降法 1000 次,以此来找到最优的 w,b,每执行一次,都将新的 w,b 带入梯度中来求,最后求得最终的 w,b,然后可以得到最终拟合的直线,即 y_pre. ```pyhon def compute_gradient(m_current, b_current, learning_rate): N = len(x) # 数据的长度 m_gradient = 0.0 b_gradient = 0.0 for i in range(N): m_gradient += -(2 / N) * x[i] * (y[i] - (m_current * x[i] + b_current)) b_gradient += -(2 / N) * (y[i] - (m_current * x[i] + b_current)) new_m = m_current - (learning_rate * m_gradient) new_b = b_current - (learning_rate * b_gradient) return new_m, new_b ``` 在 compute_gradient 函数中,主要是返回每次计算的$w,b$以及 $\frac{\partial J(\theta)}{\partial\theta}$,上面函数中 for 循环就是所求的偏导数,返回值是计算一次梯度下降时的$w,b$。 ```python plt.plot(x, y, 'ro') plt.plot(x, optimizer(), 'b-') #optimizer() plt.show() ``` 在多次计算后,再将散点图最终求得的直线图画出来即可。 ## 分析 sklearn 线性回归的官方例程 官方网站为:[Linear Regression Example](https://scikit-learn.org/stable/auto_examples/linear_model/plot_ols.html#sphx-glr-auto-examples-linear-model-plot-ols-py) ### 官方例程分析 ```python import matplotlib.pyplot as plt import numpy as np from sklearn import datasets, linear_model from sklearn.metrics import mean_squared_error, r2_score ``` 导入库 ``` diabetes = datasets.load_diabetes() # 导出数据集 ``` 导出数据集,其中 diabetes 是`sklearn.datasets.base.Bunch`类型,该类型和 Python 内置的字典类型相似 ``` diabetes_X = diabetes.data[:, np.newaxis, 2] # 分割数据集 ``` 这个用法为 sklearn 中的用法,`datasets.data`为`dataset`对象中的`data`属性,而`data`属性对应的数据为一个二维数组,故`[:, np.newaxis,2]`为取 data 中的所有行,增加一个维度,第三列,故`diabetes_X`为一个二维数组,如下: ``` {'data': array([[ 0.03807591, 0.05068012, 0.06169621, ..., -0.00259226, 0.01990842, -0.01764613], [-0.00188202, -0.04464164, -0.05147406, ..., -0.03949338, -0.06832974, -0.09220405], [ 0.08529891, 0.05068012, 0.04445121, ..., -0.00259226, 0.00286377, -0.02593034], ..., [ 0.04170844, 0.05068012, -0.01590626, ..., -0.01107952, -0.04687948, 0.01549073], [-0.04547248, -0.04464164, 0.03906215, ..., 0.02655962, 0.04452837, -0.02593034], [-0.04547248, -0.04464164, -0.0730303 , ..., -0.03949338, -0.00421986, 0.00306441]]), ``` 上面得到的 diabetes_X 的 shape 为(442, 1),再将其分为训练集和测试集 ``` diabetes_X_train = diabetes_X[:-20] diabetes_X_test = diabetes_X[-20:] ``` 该句中前 0 个到倒数第 20 个分为训练集,倒数 20 个数据为测试集。 ``` diabetes_y_train = diabetes.target[:-20] diabetes_y_test = diabetes.target[-20:] ``` 同理,将 diabetes 中的 target 属性也这样划分。 ``` regr = linear_model.LinearRegression() regr.fit(diabetes_X_train, diabetes_y_train) diabetes_y_pred = regr.predict(diabetes_X_test) ``` 然后创建一个线性模型的对象,并用训练集来 fit,最后得到预测的数据 ``` # The coefficients print('Coefficients: \n', regr.coef_) # The mean squared error print("Mean squared error: %.2f" % mean_squared_error(diabetes_y_test, diabetes_y_pred)) # Explained variance score: 1 is perfect prediction print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred)) ``` 打印出相关系数和均方误差以及差异分数 这里相关系数为$R$,回归系数为$R^2$,而回归系数 $$R^2=\frac{SSReg}{SST}=1-\frac{SSE}{SST}$$ 其中$SSReg$为回归平方和(sum of squares for regression),也叫做模型平方和,,SSE 为残差平方(sum of squares for error),SST 为总平方和(SSReg+SSE),其中各公式如下: $$SST=\sum_{i=1}^n(y_i-\bar{y})^2$$ $$SSReg=\sum_{i}(\hat{y_i}-\bar{y})^2$$ $$SSE=\sum_{i}(y_i-\hat{y})^2$$ 故在本次实验中相关系数$R$即为: $$R=\frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^n(x_i-\bar{x})^2\sum_{i=1}^n(y_i-\bar{y})^2}}$$ $\hat{y_i}$表示的为回归直线中$y$的值,$\bar{y}$表示$y$的平均值.最后结果如下:  ## 7.2 使用sklearn方法训练自己生成的数据 代码如下: ```python import matplotlib.pyplot as plt import numpy as np from sklearn import datasets, linear_model from sklearn.metrics import mean_squared_error, r2_score np.random.seed(0) x = np.linspace(0, 6, 11) + np.random.randn(11) x = np.sort(x) y = x \*\* 2 + 2 + np.random.randn(11) x=x[:,np.newaxis] print(x) regr = linear_model.LinearRegression() regr.fit(x,y) y_pre = regr.predict(x) plt.scatter(x,y) plt.plot(x,y_pre) plt.show() ``` 预测结果:  可以看到,使用sklearn的预测结果和使用梯度下降法的线性回归结果是一模一样的。 # 8 参考书目 - 机器学习实战 - 机器学习 周志华 - [线性回归理解(附纯python实现)](https://blog.csdn.net/sxf1061926959/article/details/66976356?locationNum=9&fps=1) - [sklaern官网例程](https://scikit-learn.org/stable/auto_examples/linear_model/plot_ols.html#sphx-glr-auto-examples-linear-model-plot-ols-py) ```